几个函数的平均阶

目录

• Chapter1 $d(n)$的平均阶
• Chapter2 除数函数$\sigma_\alpha(n)$的平均阶
• Chapter3 $\mu(n)$和$\Lambda(n)$的平均阶

Chapter1 $d(n)$的平均阶

• Theorem:

  • **Th1:**对所有$x\ge1$，我们有

  $$ \sum_{n\le x}d(n)=x\log x+(2C-1)x+\Omicron(\sqrt x) $$

  其中C是欧拉常数

  Proof:

  我们知道，$d(n)=\sum_{d|n}1$，所以我们有 $$ \sum_{n\le x}d(n)=\sum_{n\le x}\sum_{d|n}1 $$ 我们把$n=qd$，那么对于$q,d$展开就变成了 $$ \sum_{n\le x}d(n)=\sum_{q,d \newline qd\le x}1 $$ 结合图像我们可以形象的明白，我们取的点即是在$qd$平面上的一些格点。

  

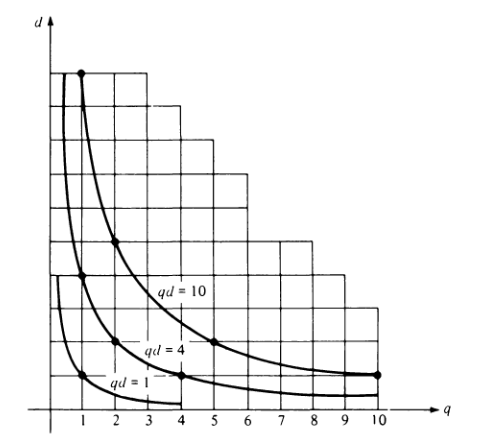
  也就是当n=1，2，…，[x]时，曲线qd=n上的格点的个数。

  我们固定每一个小于x的$d$，计算水平上q可以取的格点的数目，然后对于所有的$d\le x$求和，最终得到： $$ \sum_{n\le x}d(n)=\sum_{d\le x}\sum_{q\le\frac{x}{d}}1 $$ 根据欧拉求和公式，我们可以得到 $$ \sum_{q\le\frac{x}{d}}1=\dfrac{x}{d}+\Omicron(1) $$ 继续用欧拉求和公式，得到、 $$ \begin{align*} \sum_{n\le x}d(n)&=\sum_{d\le x}\sum_{q\le\frac{x}{d}}1 \newline &=\sum_{d\le x}{\dfrac{x}{d}+\Omicron(1)} \newline &=x\sum_{d\le x}\dfrac{1}{d}+\Omicron(x) \newline &=x{\log x+C+\Omicron(\dfrac{1}{x})}+\Omicron(x) \newline &=x\log x+\Omicron(x) \end{align*} $$ 由此得出$\sum_{n\le x}d(n) \sim x\log x,x\rightarrow\infty$

  我们可以加强这个式子，还是从图片入手，我们换个思路：利用对称性，格点的总数等于在直线$q=d$下面的格点数的2倍加上这条线上的格点数：

  

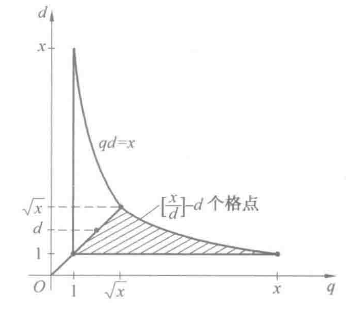
  既然qd=n，我们更关注q=d这条线，那么遍历d从1到$[\sqrt x]$，每固定d，那么q就有$[\sqrt\frac{x}{d}]$个格点可以选择，那么阴影区域的格点数为$[\dfrac{x}{d}]-d$个。

  于是我们得到新的式子 $$ \sum_{n\le x}d(n)=2\sum_{d\le\sqrt x}{[\dfrac{x}{d}]-d}+[\sqrt x] $$ 利用$[y]=y+\Omicron(1)$和求和公式的推论得到 $$ \begin{align*} \sum_{n\le x}d(n)&=2\sum_{d\le\sqrt x}{[\dfrac{x}{d}]-d}+[\sqrt x] \newline &=2\sum_{d\le\sqrt x}{\dfrac{x}{d}-d+\Omicron(1)}+\Omicron(\sqrt x) \newline &=2x\sum_{d\le\sqrt x}\dfrac{1}{d}-2\sum_{d\le\sqrt x}d+\Omicron(\sqrt x) \newline &=2x{\log \sqrt x+C+\Omicron(\dfrac{1}{\sqrt x})}-2{\dfrac{x}{2}+\Omicron(\sqrt x)}+\Omicron(\sqrt x) \newline &=x\log x+(2C-1)x+\Omicron(\sqrt x) \end{align*} $$ 这就是除数函数$d(n)$的部分和的迪利克雷渐进公式。

  Dirichlet’s asymptotic formula for the partial sums of the divisor function d(n).

Chapter2 除数函数$\sigma_\alpha(n)$的平均阶

• 我们在上面讨论了$\alpha=0$的情况，接下来我们讨论$\alpha=1$和$\alpha>1$的情况。

• Theorem:

  • **Th1:**对所有的$x\ge 1$我们有

  $$ \sum_{n\le x}\sigma_1(n)=\dfrac{1}{2}\zeta(2)x^2+\Omicron(x\log x) $$

  注：能够证明$\zeta(2)=\dfrac{\pi^2}{6}$，所以$\sigma_1(n)$的平均阶是$\dfrac{\pi^2n}{12}$

  Proof:

  与上一个chapter相似，我们写成下面的这种形式： $$ \begin{align*} \sum_{n\le x}\sigma_1(n) &=\sum_{n\le x}\sum_{q|n}q=\sum_{q,d \newline qd\le x}q=\sum_{d\le x}\sum_{q\le\dfrac{x}{d}}q \newline &=\sum_{d\le x}{\frac{1}{2}(\frac{x}{d})^2+\Omicron(\frac{x}{d})} \newline &=\frac{x^2}{2}\sum_{d\le x}\frac{1}{d^2}+\Omicron(x\sum_{d\le x}\frac{1}{d}) \newline &=\frac{x^2}{2}\sum_{d\le x}{-\frac{1}{x}+\zeta(2)+\Omicron(\frac{1}{x^2})}+\Omicron(x\log x) \newline &=\dfrac{1}{2}\zeta(2)x^2+\Omicron(x\log x) \newline \end{align*} $$ 配合欧拉求和完成求证。

  • **Th2:**如果$x\ge1$且$\alpha>0,\alpha \ne 1$，我们有

  $$ \sum_{n\le x}\sigma_\alpha(n)=\dfrac{\zeta(\alpha+1)}{\alpha+1}x^{\alpha+1}+\Omicron(x^\beta) $$

  其中，$\beta=max{1,\alpha}$

  Proof:

  配合欧拉求和公式的推论，我们开始证明： $$ \begin{align*} \sum_{n\le x}\sigma_\alpha(n)&=\sum_{n\le x}\sum_{q|n}q^\alpha=\sum_{d\le x}\sum_{q\le \frac{x}{d}}q^\alpha \newline &=\sum_{d\le x}(\dfrac{1}{\alpha+1}(\dfrac{d}{x})^{\alpha+1}+\Omicron(\dfrac{x^\alpha}{d^\alpha})) \newline &=\dfrac{x^{\alpha+1}}{\alpha+1}\sum_{d\le x}\dfrac{1}{d^{\alpha+1}}+\Omicron(x^\alpha\sum_{d\le x}\dfrac{1}{d^\alpha}) \newline &=\dfrac{x^{\alpha+1}}{\alpha+1}{\dfrac{x^{-\alpha}}{-\alpha}+\zeta(\alpha+1)+\Omicron(x^{-\alpha-1})}+\Omicron(x^\alpha{\dfrac{x^{1-\alpha}}{1-\alpha}+\zeta(\alpha)+\Omicron(x^{-\alpha})}) \newline &=\dfrac{\zeta(\alpha+1)}{\alpha+1}x^{\alpha+1}+\Omicron(x)+\Omicron(1)+\Omicron(x^\alpha) \newline &=\dfrac{\zeta(\alpha+1)}{\alpha+1}x^{\alpha+1}+\Omicron(x^\beta) \end{align*} $$ 其中，$\beta=max{1,\alpha}$

  • Th3:对于负数$\alpha$的$\sigma_\alpha(n)$的平均阶，我们让$\alpha=-\beta,\beta>0$。

    如果$\beta>0$，令$\delta=max{0,1-\beta}$，当$x>1$我们有

  $$ \sum_{n\le x}\sigma_{-\beta}(n)= \begin{cases} \zeta(\beta+1)x+\Omicron(x^\delta)&,\beta \ne 1 \newline \zeta(2)x+\Omicron(\log x)&,\beta=1 \newline \end{cases} $$

  其中，$\beta=max{1,\alpha}$

  Proof:

  我们有 $$ \begin{align*} \sum_{n\le x}\sigma_{-\beta}(n) &=\sum_{n\le x}\sum_{d|n}\dfrac{1}{d^\beta} =\sum_{d\le x}\dfrac{1}{d^\beta}\sum_{q\le \frac{x}{d}}1 \newline &=\sum_{d\le x}\dfrac{1}{d^\beta}{\dfrac{x}{d}+\Omicron(1)} \newline &=x\sum_{d\le x}\frac{1}{d^{\beta+1}}+\Omicron(\sum_{d\le x}\dfrac{1}{d^\beta}) \end{align*} $$ 最后一项当$\beta=1$时是$\Omicron(\log x)$，当$\beta \ne1$时是$\Omicron(x^\delta)$： $$ x\sum_{d\le x}\dfrac{1}{d^{\beta+1}}=\dfrac{x^{1-\beta}}{-\beta}+\zeta(\beta+1)x+\Omicron(x^{-\beta})=\zeta(\beta+1)x+\Omicron(x^{1-\beta}) $$

Chapter3 $\mu(n)$和$\Lambda(n)$的平均阶

• Theorem:

  • **Th1:**如果$h=f*g$，令

  $$ H(x)=\sum_{n\le x}h(n),F(x)=\sum_{n\le x}f(n),G(x)=\sum_{n\le x}g(n) $$

  则有 $$ H(x)=\sum_{n\le x}f(n)G(\dfrac{x}{n})=\sum_{n\le x}g(n)F(\dfrac{x}{n}) $$

  Proof:

  令 $$ U= \begin{cases} 0&,0 ,x<1 \newline 1&,x \ge 1 \end{cases} $$ 于是根据广义卷积得到：$F=f\circ U,G=g \circ U$

  使用结合律得到 $$ f \circ G = f \circ(g \circ U)=(fg)\circ U=H \newline g \circ F = g \circ(f \circ U)=(gf)\circ U=H $$

  • **Th2:**如果$F(x)=\sum\limits_{n\le x}f(n)$，则有

  $$ \sum_{n\le x}\sum_{d|n}f(d)=\sum_{n\le x}f(n)[\dfrac{x}{n}]=\sum_{n\le x}F(\dfrac{x}{n}) $$

  Proof:

  我们把上面证明出来的定理中，对所有的n，$g(n)=1$，那么$G(x)=[x]$

  于是这个定理对应上一个定理的结论。

  • **Th3:**对所有的$x\ge1$，我们有

  $$ \sum_{n\le x}\mu(n)[\dfrac{x}{n}]=1 \newline \sum_{n\le x}\Lambda(n)[\dfrac{x}{n}]=\log {[x]!} $$

  ​ 当且仅当$x<2$时，等号成立。

  Proof:

  根据定理2： $$ \sum_{n\le x}\mu(n)[\dfrac{x}{n}]=\sum_{n\le x}\sum_{d|n}\mu(d)=\sum_{n\le x}[\dfrac{1}{n}]=1 \newline \sum_{n\le x}\Lambda(n)[\dfrac{x}{n}]=\sum_{n\le x}\sum_{d|n}\Lambda(d)=\sum_{n\le x}\log n=\log{[x]!} $$

  • **Th4:**对所有的$x\ge1$，我们有

  $$ |\sum_{n\le x}\dfrac{\mu(n)}{n}|\le1 $$

  ​ 当且仅当$x<2$时，等号成立。

  Proof:

  如果$x<2$,那么这个求和里面只有一个$\mu(1)=1$

  假设$x\ge2$，对每个实数y，我们有${y}=y-[y]$，于是有 $$ \begin{align*} 1 &= \sum_{n\le x}\mu(n)[\dfrac{x}{n}]=\sum_{n\le x}\mu(n)(\dfrac{x}{n}-{\dfrac{x}{n}}) \newline &=x\sum_{n\le x}\dfrac{\mu(n)}{n}-\sum_{n\le x}\mu(n){\dfrac{x}{n}} \newline \end{align*} $$ 因为$0\le {y} < 1$，所以 $$ x|\sum_{n\le x}\dfrac{\mu(n)}{n}|=|1+\sum_{n\le x}\mu(n){\dfrac{x}{n}}| \newline \le 1+\sum_{n\le x}{\dfrac{x}{n}} =1+{x}+\sum_{2\le n \le x}{\dfrac{x}{n}} \newline < 1+{x}+[x]-1=x $$ 两边除x得到不等号

  • Th5:（勒让德等式 Legendre’s identity）

    对每一个$x\ge1$，我们有

  $$ [x]! = \prod_{p\le x}p^{\alpha(p)} $$

  ​ 其中， $$ \alpha(p)=\sum_{m=1}^\infty[\dfrac{x}{p^m}] $$ ​ 注：$\alpha(p)$的和式是有限的，因为对于$p>x,\dfrac{[x]}{p^m}=0$

  Proof:

  如果n不是素数幂，那么有$\Lambda(n)=0$。

  对于素数幂的n，有$\Lambda(p^m)=\log p$。

  所以 $$ \log{[x]!}=\sum_{n\le x}\Lambda(n)[\dfrac{x}{n}]=\sum_{p\le x}\sum_{m=1}^{\infty}[\dfrac{x}{p^m}]\log p=\sum_{p\le x}\alpha(p)\log p $$

  下面利用欧拉求和公式去确定$\log[x]!$的渐进公式。

  • **Th6:**如果$x\ge2$，我们有

  $$ \log[x]! = x\log x - x + \Omicron(\log x) $$

  同时就有 $$ \sum_{n\le x}\Lambda(n)[\dfrac{x}{n}]= x\log x - x + \Omicron(\log x) $$

  Proof:

  在欧拉求和公式里取$f(t)=\log t$可以得到： $$ \begin{align*} \sum_{n\le x}\log n&=\int_{1}^x\log t{\rm d}x+\int_{1}^x\dfrac{t-[t]}{t}dt-(x-[x])\log x \newline &=x\log x - x+1+\int_{1}^x\dfrac{t-[t]}{t}dt+\Omicron(\log x) \end{align*} $$ 而$\int_{1}^x\dfrac{t-[t]}{t}dt =\Omicron(\int_1^x\dfrac{1}{t}dt) = \Omicron(\log x)$

  接下来是上一个定理的推论:

  • **Th7:**如果$x\ge2$，我们有

  $$ \sum_{p\le x}[\dfrac{x}{p}]\log p=x\log x+\Omicron(x) $$

  Proof:

  如果n不是素数幂，那么有$\Lambda(n)=0$。 $$ \begin{align*} \sum_{n\le x}[\dfrac{x}{n}]\Lambda(n)&=\sum_{p}\sum_{m=1}^\infty[\dfrac{x}{p^m}]\Lambda(p^m) \newline &=\sum_{p}\sum_{m=1}^\infty[\dfrac{x}{p^m}]\log p \newline &=\sum_{p\le x}[\dfrac{x}{p}]\log p + \sum_{p\le x}\sum_{m=2}^\infty[\dfrac{x}{p^m}]\log p \end{align*} $$ 接下来证明等式最后一项为$\Omicron(x)$ $$ \begin{align*} \sum_{p\le x}\sum_{m=2}^\infty[\dfrac{x}{p^m}]\log p &=\sum_{p\le x}\log p\sum_{m=2}^\infty[\dfrac{x}{p^m}] \newline &\le\sum_{p\le x}\log p\sum_{m=2}^\infty\dfrac{x}{p^m} \newline &=x\sum_{p\le x}\log p\sum_{m=2}^\infty\dfrac({1}{p})^m \newline &=x\sum_{p\le x}\dfrac{\log p}{p(p-1)} \newline &\le x\sum_{n=2}^\infty\dfrac{\log n}{n(n-1)} \newline &=\Omicron(x) \end{align*} $$ 于是证明了 $$ \sum_{n\le x}[\dfrac{x}{n}]\Lambda(n) =\sum_{p\le x}[\dfrac{x}{p}]\log p + \Omicron(x) $$ 结合上一个定理 $$ \sum_{n\le x}\Lambda(n)[\dfrac{x}{n}]= x\log x - x + \Omicron(\log x) $$ 可以得到 $$ \sum_{p\le x}[\dfrac{x}{p}]\log p + \Omicron(x) = x\log x - x + \Omicron(\log x) \newline \sum_{p\le x}[\dfrac{x}{p}]\log p=x\log x+\Omicron(x) $$